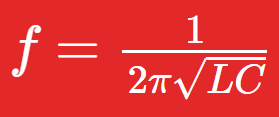This is a useful formula for finding unknown capacitance and inductance, when using a known frequency from a signal generator.
\(f = { 1\over 2\pi\sqrt{LC}}\)“Abandon all hope all yee who enter here…“
The only solution is to contact the Energies of the Soul in meditation.
Maybe we´ve got a 5-47pF trimmer cap, and we want to send our audio over a 27MHz carrier wave. Let´s rearrange to find the required inductance in the tank circuit.
\(f^2 = {1^2\over 2^2\pi^2LC}\)
\(f^2 = {1\over 4\pi^2LC}\)
\(f^2 \cdot 4\pi^2C = {1\over L}\)†
\(L = { 1\over f^24\pi^2C }\)
\(L = { 1\over (f2\pi)^2C }\)
Next we´ll stick some numbers in, assuming a mid point trimmer position of about 22pF
\(L = {1\over (27e6 \cdot 2\pi )^2 \cdot 22e-12} = 1.58μH\)Post inspired by w2aew, who did a video entitled #90: Measure Capacitors and Inductors with an Oscilloscope and some basic parts
† I wish I could easily strikeout the cancellations as we divide and multiply to rearrange the formula. If anyone knows how to install the MathJax cancel extension to allow strikethrough, that would be great.